Second-order processes

Second-order processes are those whose dynamics are represented by second-order differential equations. The standard form for these equations is:

where is known as the natural period of oscillation, as the damping factor, and K as the steady-state gain.

NB: the standard form for the second-order equation isn't as useful as it is for first-order equations. The only information that's directly useful is the steady-state gain.

The polynomial which is formed from the coefficients of the terms in y, in this case

is called the characteristic equation and has an important influence on the solution. There are three possible solutions for the step response of processes described by this equation and the one which applies in a particular instance depends on the roots of the characteristic equations. These roots can be obtained using the normal quadratic solution formula:

the three possible scenarios are:

Two real, distinct roots

This occurs when > 1.

In this case the solution to a unit step (step size 1) is given by

and the response, shown below at a variety of different damping factors, is called an overdamped second-order response.

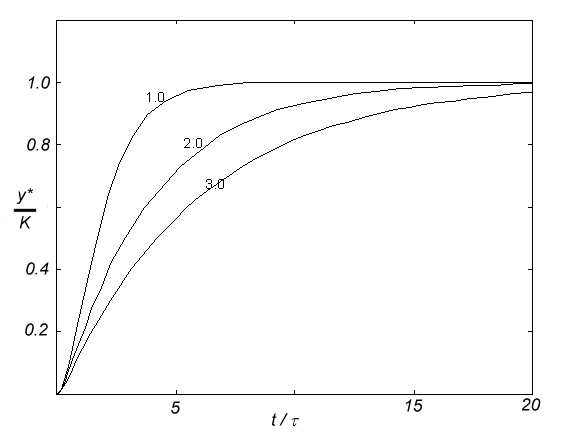
The key features to notice about this response are

• The response takes time to build up to its maximum gradient.
• The larger the damping factor the more sluggish the rate of response
• Regardless of the damping factor, all the responses head towards the same final steady-state value.

Two real, but equal roots

This situation occurs when = 1.

The solution for a unit step is

This solution is plotted along with the overdamped responses on the graph above. The response looks very similar to the overdamped responses, but represents the limiting case - it is the fastest form of this non-oscillatory response and is called critical damping.

Two complex conjugate roots

When < 1 two complex conjugate (a + ib, a- ib) roots are obtained and these lead to the following response for a unit step

This response, shown below, is called an underdamped second-order response to a unit step.

Some important features of this response are

• The response doesn't go at its fastest immediately - it takes time to build up speed.
• As the damping factor falls away from 1 the response becomes faster and more oscillatory, and the amount of overshoot increases. At damping factors close to 1 (0.8 in the figure) no real oscillation can be seen, but there is still a little overshoot.
• Regardless of the damping factor, all the responses settle at the same final steady-state value (determined by the steady-state gain of the process)

A MathCad toy that lets you play with different combinations of damping factors and natural periods can be found here. (NB this will only work on computers with MathCad 13.1 or above installed)

Important Note

Do NOT attempt to memorise any of the solutions for second-order response to a step change. You will not be required to regurgitate them in an exam. You will not be asked to derive them ( it takes several pages of algebra).

What you will have to know is the effect that the type of roots of the characteristic equation have on the shape of the process response. You can get these roots by directly factorising the second-order equation - you don't need to work out the value of the damping factor, just the values of the roots. In control problems this will save you an awful lot of heartache!