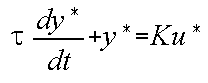
A first-order process is one whose dynamics can be represented by a first-order differential equation, i.e.
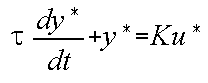
Linear first-order differential equations can be solved by a number of methods - you should consult your maths textbooks for details. The solution of the standard form of the equation (given above) to a step input of A units is given by
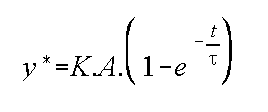
The constant K is known as the steady-state gain, and ![]() is called the time constant.
is called the time constant.
This response is plotted below
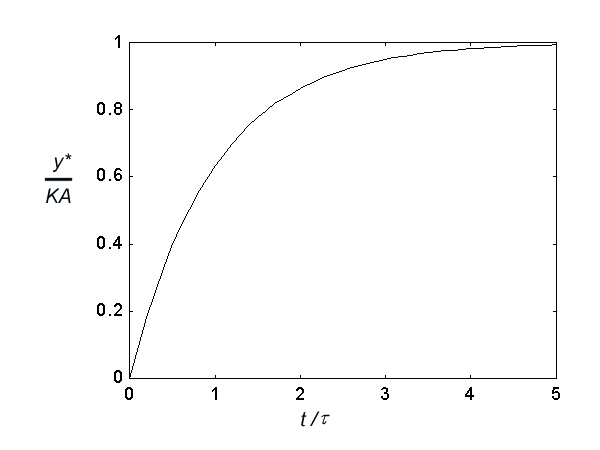
Now, lets look at the time based response to the step change. First of all, the only factor which affects the dynamic, or time-based, behaviour of the response is the time constant, . The larger the value of the time constant the slower the response. By simply inserting values into the equation above, it is possible to calculate that after one time constant the response will be approximately 63% complete, and that after 3 time constants the response will be approximately 95 % complete. Although, analytically, the response will only get to its final value after an infinite time has passed, for practical purposes all change ceases after five time constants ( the response is 99% complete ).
The size of the final steady-state change is decided by the steady-state gain, K, and the size of the change in input.
Thus, given this general knowledge of first-order step response you should be able to say quite a lot about the step response of a first-order system just by looking at the differential equation.